三相推理是佛教量学、因类学中有关真实比量的一种论式,凡是符合这种论式的推理,决定符合真相,不会有任何的错误,学会了这种比量,很容易就能发现自他所说的话中,哪些是真的,哪些是假的。
一个合格的论式,首先必须具足四要素:
有法(或者叫所诤事)和立宗(或者叫所立)、因以及比喻。
简称为三部分,即:宗、因、喻。
有法就是我们所要讨论的对象;我们要建立这个有法具有某种属性、特征的观点,所建立的观点就叫做立宗;要建立成这个观点,一定要有理由,这个就叫做因。这个论证还要通过某种比喻让别人容易明白,而且这个比喻自他双方都承认,这就是喻。
而三相推理所包含的三相如下:
(1) 有法在因上成立
(2) 同品周遍
(3) 异品周遍
举例来说明一下:
嬴政会死,是人故。如苏格拉底。
有法:嬴政这个人;
立宗:嬴政会死;
因:嬴政是人;
比喻:就像苏格拉底会死那样。
接下来分析这个推导是否满足三相推理:
(1) 有法在因上成立
嬴政是不是人?当然是。读过上一篇《结合现代集合论说说因明九句因》的同学会想起集合的描述方法,即:嬴政这个元素属于人类这个集合。设人类这个集合为A(因),嬴政用x表示,有x∈A。好了,第一相满足。
(2) 同品周遍
同品周遍就要因在宗遍成立。观察因上成立的所有法都在宗上成立。如果用集合的观点来看就是所有属于因这个集合的元素都属于宗这个集合。在这里,宗这个集合可以表述为所有会死的事物。从九句因的角度看,同品周遍要成立,一定是九句因的第2或8相。以本例来说是第8相(同品部分有,异品没有。第8相更具代表性,先以其为例进行讨论)。绘图如下。A表示因:人类。B表示宗:会死的事物。
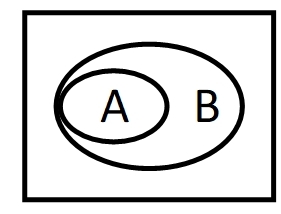
(3) 异品周遍
异品周遍是指宗的异品遍成立于因的异品。上例中,宗的异品就是:不死的事物,因的异品是:不是人的事物。要异品周遍就要成立所有不死的事物都不是人。
用集合的说法讲就是宗的补集,全都属于因的补集。作图表示如下。蓝色部分为宗的异品。
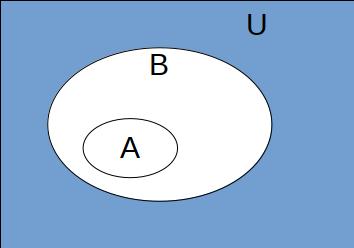
而下图中橙色部分为因的异品。
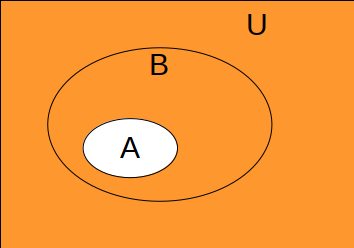
显然橙色部分是一定包含蓝色部分的。即同品周遍时,异品一定周遍(九句因第2项同样推导)。其实数学中也有一个结论就是:一个命题成立,其逆否命题一定成立。我们的因和立宗其实就是一个命题。
那第三相推理就不必要了吗?
个人认为并不是这样,原因有二:
(1) 我们要看看我们做三相推理的场景往往不会是我们现在举的例子这么简单,在面对具体问题的时候,我们不能够在第一时间得到因和宗的清晰边界,所以需要对其进行考察,对讨论的各种法进行观察,讨论各种元素的归属。而单向思维的考察方式有出错的可能,这是第三相具备的检查复核的意义。
(2) 利用三相推理做同品周遍推导的时候,并没有明确或显示表达讨论对象的全集是什么。也就是上面图中方框所表示的集合并未做观察和澄清。图中方框表示全集U,在因明的讨论范畴,它通常是指有实法。但是在整个佛法的讨论范畴中,这个边界条件可能变动,有可能包含心法,有可能又要讨论无实法等等。而这第三相的意义就是帮助我们明确了这个暗设的讨论前提,并让我们清晰明了地排除交流过程中因为暗设前提带来的问题。我想这是异品周遍最重要的意义所在。
当然,数学中所讲到的,在绝对清晰的描述和全集清晰定义的情况下,确实须要承许:一个命题等价于其逆否命题。
综上所述,个人认为异品周遍在佛法的讨论中是非常有必要的。